Magnetization Features: Magnetic Moment, Dipole, and Models
Magnetization of magnets involves understanding the fundamental properties such as magnetic moments, dipoles, and various models that describe their behavior. Let’s learn about these concepts in this article.
 [1]
[1]
Magnetic Moment
A magnetic moment is a vector quantity that represents the magnetic strength and orientation of a magnet or a magnetic particle.
- The magnetization of a magnetized material is the local value of its magnetic moment per unit volume, usually denoted M, with units A/m.
- It is a vector field, rather than just a vector (like the magnetic moment), because different areas in a magnet can be magnetized with different directions and strengths (for example, because of domains, see below).
For example, a good bar magnet may have a magnetic moment of magnitude 0.1 Am2 and a volume of 1 cm3, or 0.000001 m3, and therefore an average magnetization magnitude is 100,000 A/m. Iron can have a magnetization of around a million A/m. Such a large value explains why magnets are so effective at producing magnetic fields.
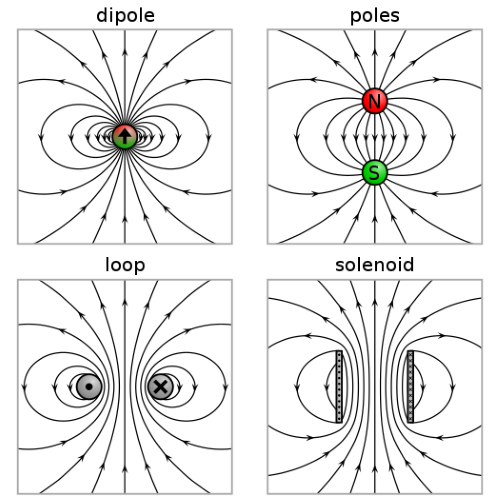
Magnetic Dipole
A magnetic dipole is a simple magnetic system with two opposite poles (north and south) separated by a small distance. Magnetic dipoles align themselves with external magnetic fields to minimize energy, creating a torque that tries to align the dipole with the field.
Although for many purposes it is convenient to think of a magnet as having distinct north and south magnetic poles, the concept of poles should not be taken literally: it is merely a way of referring to the two different ends of a magnet. The magnet does not have distinct 'north' or ‘south’ particles on opposing sides. (No magnetic monopole has yet been observed.) If a bar magnet is broken in half, in an attempt to separate the north and south poles, the result will be two bar magnets, each of which has both a north and south pole.
Magnetization Models
Let’s start with the two most classic models.
- Gilbert model: If the magnetic pole distribution is known, then outside the magnet the pole model gives the magnetic field exactly. This pole model is also called the 'Gilbert model' of a magnetic dipole. Griffiths suggests (p. 258): 'My advice is to use the Gilbert model, if you like, to get an intuitive 'feel' for a problem, but never rely on it for quantitative results.'
- Ampere model: Another model is the 'Ampere model', where all magnetization is due to the effect of microscopic, or atomic, circular 'bound currents', also called 'Amperian currents' throughout the material. For a uniformly magnetized cylindrical bar magnet, the net effect of the microscopic bound currents is to make the magnet behave as if there is a macroscopic sheet of electric current flowing around the surface, with local flow direction normal to the cylinder exit-hand rule telling which direction the current flows. The Ampere model gives the exact mas. The magnetic field is both inside and outside the magnet. It is usually difficult to calculate the Amperian currents on the surface of a magnet, whereas it is often easier to find the effective poles for the same magnet.
Other Magnetization Features
- Magnetic Flux Density (B) is the measure of the strength and direction of the magnetic field at a specific point. It is measured in Tesla (T) or Gauss (G), where 1 Tesla equals 10,000 Gauss.
- Coercivity (Hc) refers to the intensity of the applied magnetic field required to reduce a magnet's magnetization to zero after the material has been driven to saturation. This property is measured in Amperes per meter (A/m) or Oersted (Oe).
- Temperature Coefficients indicate how the magnetic properties of a material change with temperature. These coefficients are typically expressed as a percentage change per degree Celsius (%/°C).
- Energy Product (BHmax) represents the maximum energy density stored in a magnetic material. It is measured in MegaGauss-Oersteds (MGOe) or Joules per cubic meter (J/m³).
Take the case of N35 and N52 neodymium magnets:
|
Property |
N35 Nd Magnets |
N52 Nd Magnets |
|
Magnetic Flux Density (B) |
1.17 - 1.21 Tesla (11,700 - 12,100 Gauss) |
1.42 - 1.48 Tesla (14,200 - 14,800 Gauss) |
|
Coercivity (Hc) |
955 kA/m (12,000 Oe) |
876 kA/m (11,000 Oe) |
|
Temperature Coefficients |
-0.12% per degree Celsius |
-0.11% per degree Celsius |
|
Energy Product (BHmax) |
33-35 MGOe (264-280 kJ/m³) |
48-52 MGOe (384-416 kJ/m³) |
|
Magnetic Moment |
Approximately 1.17 A·m² for a 1 cubic centimeter volume |
Approximately 1.42 A·m² for a 1 cubic centimeter volume |
Conclusion
Understanding magnetization features such as magnetic moments, dipoles, and the various models is crucial for effectively utilizing magnets in practical applications. The choice between these magnets will depend on specific requirements, including the need for magnetic strength, temperature stability, and resistance to demagnetization.
By grasping these fundamental concepts, we can better harness the potential of magnetic materials in various technological and industrial fields. For more information, please check Stanford Magnets.
Reference:
[1] Magnetic dipole. (2024, January 12). In Wikipedia. https://en.wikipedia.org/wiki/Magnetic_dipole















